Auckland Sports College

"Moving Forward Together"

Calculus - Level 3 Complex Numbers

Immediately below this paragraph is a table with links to the exam questions and answers for all the externals way back to 2013. Focus on the exams for the last three years. Recognise the type of question e.g This is a question about..... Know how you are going to set out your working when answering each type of question.

Year	Complex Numbers

2023	Questions	Answers
2022	Questions	Answers
2021	Questions	Answers
2020	Questions	Answers
2019	Questions	Answers
2018	Questions	Answers
2017	Questions	Answers
2016	Questions	Answers
2015	Questions	Answers
2014	Questions	Answers
2013	Questions	Answers

Complex Numbers

We use the Walker maths revision book. This external standard is worth 5 credits. It is an algebra standard and the Walker maths booklet is very good for revising (or learning for the first time) the algebra that is useful in this standard.

1. Expanding Brackets
 
This is an algebra exam and sometimes you will be asked something without an 'i' in sight. From the 2023 exam
.
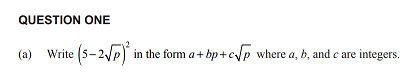
This expands to 25 + 4p - 20p^1/2
Expanding brackets is dealt with on p7 of Walker
 
2. Quadratic Formula
 
Here is another question without an 'i' in sight. Q1b from the 2023 exam

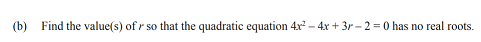
The discriminant is b² - 4ac
If the discriminant is greater than zero the quadratic has two real roots.
If the discriminant equals zero the quadratic has one real root.
If the discriminant is less than zero the quadratic has no real roots.
 
In this question b = -4, a = 4, and c = 3r -2
So the discriminant is 16 - 4*4*(3r-2) = 16 - 48r + 32
This is less than zero if 48r - 48 < 0 i.e if r < 1
 
The quadratic formula is dealt with on p8 of Walker
 
3. Equations involving Surds
 
Yet another question without an 'i' in sight. Q3c from the 2023 exam

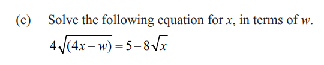
This is an ugly looking equation. It is a 'merit' question
. There is only one square root on each side, so square both sides.
 
16(4x - w) = 25 - 80x^1/2 + 64x
64x - 16w = 25 - 80x^1/2 + 64x
-16w = 25 - 80x^1/2 and we need to make 'x' the subject, so
80x^1/2 = 25 - 16w
x^1/2 = (25-16w)/80
x = ((25-16w)/80)²
 
It is useful to be able to simplify fractions containing a square root.
 
Remember: (20)^1/2 = 4^1/25^1/2 = 2x5^1/2
 
AND : 15^1/2/27^1/2 = (15/27)^1/2 = (5/9)^1/2 = 5^1/2/3
 
Surds are covered on pages 24-34 of Walker
 
4. The Remainder Theorem
 
When a polynomial f(x) is divided by (x - a) the remainder is f(a)
 
if f(a) = 0 then (x-a) is is a factor of f(x). You already know this. It is called the factor theorem.
 
Here is another question without an 'i' in sight. Q3a from the 2023 exam

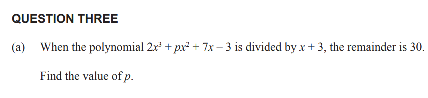
f(-3) = 30
-54 +9p -21 -3 = 30
9p = 108
p = 12
 
The remainder theorem is covered on p49 of Walker
 
5. Adding and Subtracting Complex numbers
 
This is easy. Add the real parts and add the imaginary parts separately.
 
(4 + i) + (7 - 5i) = 11 - 4i
(4 + i) - (7 - 5i) = -3 + 6i
 
6. Multipying Complex numbers
 
Expand the brackets, but remember i² = -1
 
(4 + i)*(7 - 5i) = 28 - 20i + 7i +5 = 33 - 13i
 
Multiplication of complex numbers in rectangular form is dealt with on p57 of Walker
 
You can multiply and divide complex numbers using your graphics calculator Practice this before exam day!
 
7. Dividing Complex numbers
 
If u = x + yi, then the conjugate of u, ū is x - yi
 
To divide a complex number by a complex number, multiply the fraction by ū/ū
 
This works because u*ū is a real number
 
Division of complex numbers in rectangular form is dealt with on p61 of Walker
 
This is Question 3b from the 2023 exam
 

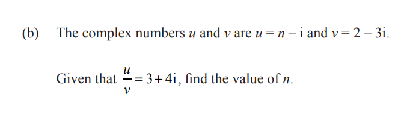
One way of answering is to multiply by the conjugate

 
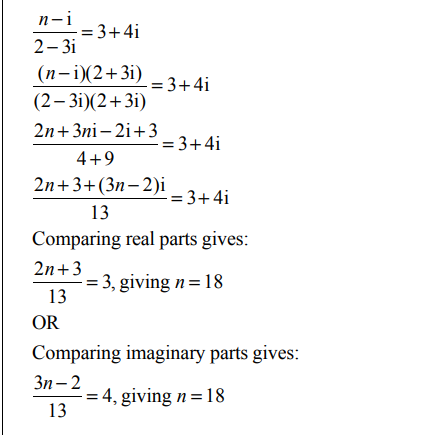
Another way of answering this question is to mulyiply both sides by 2-3i to get
n - i = (3+4i)(2-3i)= 6 - 9i + 8i +12 = 18 -i, n =18 (equating the real parts)
 
Division of complex numbers is covered on p61 of Walker
 
8. Solving Quadratic Equations by 'completing the square'
 
Completing the square is dealt with on pages 35 and 71, of Walker
 
(a + b)² = (a + b)(a + b) = a² + 2ab + b²
 
So, in a quadratic ax² + bx + c when the co-efficient 'b' of 'x' is an even number, the quadratic can be rewritten as (a + b/2)² -(b/2)² + c
 
This can be useful in solving quadratics where both roots are complex. This is question 3b from the 2022 exam

 
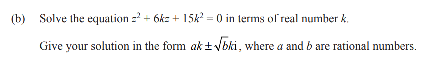
In this question b² - 4ac = 36k² - 60k² which is less than zero as k² must be positive
 
As 6k is even the quadratic can be rewritten as
 
(z + 3k)² - 9k² + 15k² = (z+3k)² + 6k² = 0
 
This simplifies to
 
(z + 3k)² = -6k²
 
Taking square roots of both sides, z + 3k = ±6²ki
 
z = -3k ±6^1/2ki
 
9. Solving cubics when you are given one real root
 
Solving cubics is covered on pages 75-77, of Walker
 
This is question 2c from the 2022 exam

 
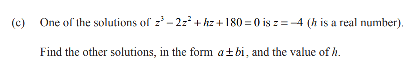
As z = -4 is a solution f(-4) = 0, so -64 - 32 -4h +180 = 0, 4h = 84, h = 21
 
Long division is used to find the quadratic which when multiplied by (x+4) gives z³ - 2z² + 21z + 180
 

 
and now it is a matter of finding the roots of z² - 6z + 180 = 0
 
These roots are both complex as the discriminant, b² - 4ac = 36 - 720 is less than zero
 
So, completing the square gives
 
(z - 3)² = -36
 
z = 3 ±6i
 
10. Solving cubics when you are given one complex root
 
Solving cubics is covered on pages 75-77, of Walker
 
This is question 1d from the 2023 exam

 
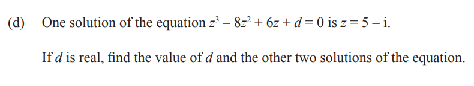
Complex roots come in pairs. If 'z' is a root then the conjugate of 'z' is also a root.
 
So, if z = 5-i is a solution so is z = 5 + i.
 
If 5-i is a solution then (z - 5 + i) is a factor
 
In this question (z - 5 - i) and (z - 5 + i) are both factors
 
Multiply them together (z - 5 - i)(z - 5 + i) = z² - 5z + zi - 5z + 25 - 5i -zi + 5i +1 = z² - 10z + 26
 
So now, find what you multiply z² - 10z + 26 by to get z³ - 8z² + 6z + d
 
z(z² - 10z + 26) = z³ - 10z² + 26z
 
Subtracting
  z³ - 8z² + 6z + d
-(z³ - 10z² + 26z)
 
The remainder is 2z² - 20z + d
 
This is 2 times z² - 10z + 26 if d = 52
 
So the third factor is 'z + 2'
 
The other two solutions are z = 5 +i and z = -2, 'd' = 52
 
11. Argand Diagrams - Polar and Rectangular forms
 
Complex numbers can be represented on an x-y plane, where the x-axis is called the Real axis and the y-axis is called the imaginary axis.
 
This is question 3a from the 2022 exam

 
r = 3 + 2i and s = 2 - 5i so v = 2r - s = 6 + 4i - 2 + 5i = 4 + 9i
To get the mark for this question you also had to mark 'v' at (4,9) on the diagram
 
This way of representing a complex number as 'along and up' is called 'rectangular form'. An alternative way to get to a complex number 'z' on an Argand diagram is to travel along a bearing (an angle from the positive Real axis) for a set distance (the modulus).
 

 
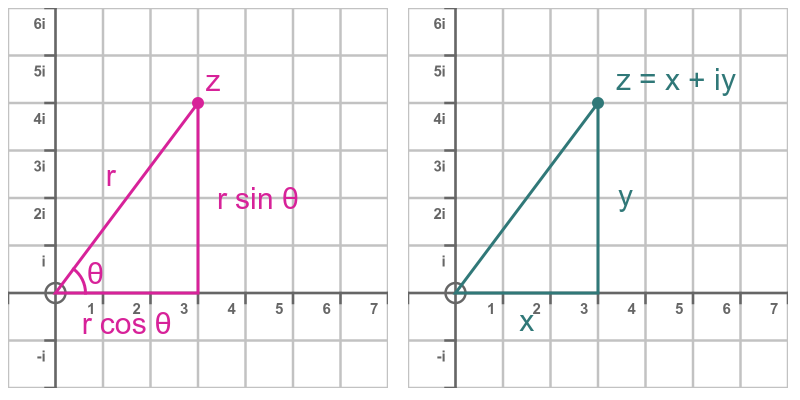
The distance 'r' is the hypotenuse of the right angle triangle whose other sides have length 'x' and 'y'.
 
The distance 'r' is called the modulus. The notation is ∣z∣
 
∣z∣ = (x² + y²)^1/2
 
The distance x = rcosΘ and the distance y = rsinΘ so the complex number z = rcosΘ + irsinΘ
 
This is abbreviated to rcisΘ, the polar form of the complex number
 
The angle Θ is the argument of 'z', abbreviated as arg(z)
 
tanΘ = y/x so arg(z) = tan^-1(y/x)
 
Argand diagrams are covered on page 56 of Walker. Polar form is covered on page 81.
 
Your calculator can be used to convert between rectangular and polar forms. Practice this before the exam. Make sure you can convert rectangular form to polar form without a calculator.
 
12. Modulus, argument, and special triangles
 
This is question 2b from the 2023 exam

 
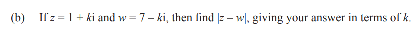
z - w = 1 + ki - 7 +ki = -6 + 2ki
 
So, ∣(z -w)∣ = (6² + 2k²)^1/2 = (36 + 4k²)^1/2
 
This is question 2c from the 2023 exam

 
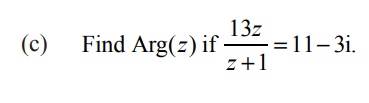
There are a few ways of approaching this question. We could start by multiplying both sides by 'z+1'
 
13z = (z+1)(11-3i) = 11z - 3zi + 11 - 3i
 
2z + 3zi = 11 - 3i
 
Replacing 'z' with x + yi
 
2x + 2yi + 3xi - 3y = 11 - 3i
 
Equating real and imaginary parts 2x - 3y = 11 and 2y + 3x = -3
 
x = 1, y = -3
 
Θ = tan^-1-3 = -1.25rad
 
This is question 1c from the 2022 exam

 
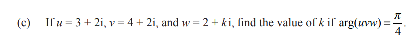
The trick to this question is realising that if Θ is 45 degrees, the triangle is isoceles and x = y i.e the real part equals the imaginary part.
 
uvw = (3+2i)(4+2i)(2+ki)
= (8+14i)(2+ki)
= 16 - 14k + 8ki + 28i)
 
and as the real parts and the imaginary parts are equal
 
16 - 14k = 28 + 8k, k = -12/22 = -6/11
 
13. Multiplying and Dividing Complex numbers in polar form
 
To multiply complex numbers in polar form, multiple the moduli and add the angles
 
To divide complex numbers in polar form, divide the moduli and subtract the angles
 
Multiplication and division of complex numbers in polar form is covered on page 87 of Walker This is question 2a from the 2023 exam

 
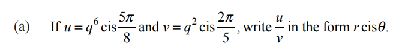
u/v = q^6-2cis(5Π/8 - 2Π/5) = q⁴cis(9Π/40)
 
14. De Moivre's theorem and solving complex number cubics and quartics
 
De Moivre's theorem and its use to solve polynomial equations in polar form is covered in Walker from pages 93-102
 
De Moivre's theorem states that (rcisΘ)ⁿ = rⁿcisnΘ
 
We are interested in it expressed this way, if zⁿ = rcisΘ then z = r^1/ncis(Θ/n)
 
BUT there are 'n' roots. Complex roots are distributed evenly around a circle of radius r^1/n. So if the equation is a cubic the roots are 2Π/3 apart. Once you have found the first root add 2Π/3 to the angle to get the second root (z₂). Than add another 2Π/3 to the angle to get z₃
 
If the equation is a quartic the roots are Π/2 apart
 
This is question 2d from the 2023 exam

 
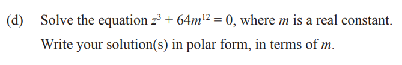
The first thing is to determine Θ. The modulus of zⁿ is 64m¹²
 
In rectangular form z³ =-64m¹² + 0i, so Θ is Π.
 
The polar form of this polynomial is z³ =64m¹²cisΠ
 
and z₁ = 4m⁴cisΠ/3
 
z₂ = 4m⁴cis(Π/3 + 2Π/3) = 4m⁴cis(Π)
 
z₃ = 4m⁴cis(Π + 2Π/3) = 4m⁴cis(5Π/3)
 
15. Find the locus of complex numbers where the real or imaginary part is restricted
 
This is covered in Walker on page 103
 
16. Find the locus of complex numbers where the modulus is restricted
 
This is covered in Walker on page 106
 
This is question 2e from the 2022 exam

 
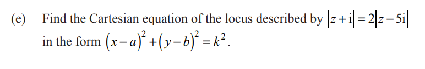
(x² + (y+1)²)^1/2 = 2(x²+(y-5)²)^1/2
 
squaring both sides
x² + (y+1)² = 4x²+4(y-5)²
 
x² + y² + 2y +1 = 4x²+4y² - 40y + 100
 
3x² + 3y² - 42y + 99 = 0
 
x² + y² - 14y + 33 = 0
 
completing the square for 'y'
 
x² + (y - 7)² = 16
 
17. Find the locus of complex numbers where the argument is restricted
 
This is covered in Walker on pages 110-112
 
18. Excellence Questions that are just tedious algebra